This article is about MicroStation® Visual Basic for Applications (VBA). It's written for developers using Bentley Systems MicroStation. Questions similar to this appear on the Be Communities Forums. This problem appeared in the MicroStation Programming Forum.

Introduction

The term Regression Analysis covers various types of numerical analysis. In the context of MicroStation, it concerns the analysis of point data, and how to represent those data with a best-fit line or curve.

MicroStation provides several development tools, of which the simplest and quickest is Visual Basic for Applications (VBA). VBA is a Rapid Application Development (RAD) tool, which Bentley Systems license from Microsoft. You can use VBA to write your own regression analysis tools.

Performance Considerations

If you have large numbers of points to analyse, then VBA may not be the best solution. While VBA is an excellent tool for prototyping a solution, it's not the best performing language when it comes to numerical analysis.

The fastest code is created using C++ to handle large and complex data structures, compiled to a native code executable or DLL. Native code runs fastest and makes best use of computer memory.

The Regression Analysis application is an example of a native-code application. It's optimised for regression analysis of a larger number of points than VBA can handle, and it works in both 2D and 3D.

Questions about Regression Analysis

These questions were posted to the Be Communities MicroStation Forum.

• How can I fit points to a straight line?
• How can I fit points to a circle?

Q   How can I fit my survey points to a straight line in MicroStation?

A   MicroStation does not provide any regression analysis tools. However, some of the add-on applications may offer tools in that category for specific workflows. This example shows how to write code to perform a linear best-fit. You may have survey points that you want to use to create a best-fit line …

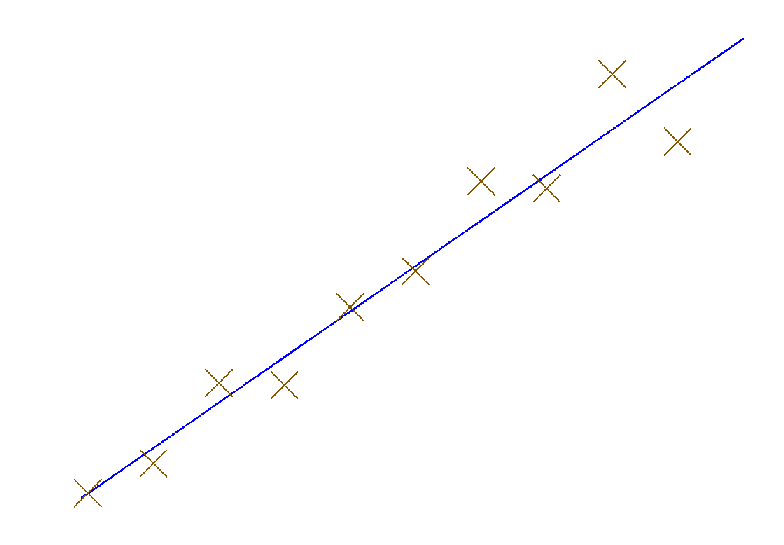
Least Squares Fit

The Least Squares algorithm calculates the coefficients of a linear equation that passes through a set of points. The form of the equation is y = mx + b where m and b are constants and x and y are variables.

Here's a subroutine that analyses an array of data points. It uses a least-squares algorithm to calculate the linear coefficients m and b. With those constants available, it's trivial to create a line element to illustrate the calculation. Here's the code …

' ---------------------------------------------------------------------
'   LeastSquareAnalysis
'   Provides a solution to the equation Y = M * X + B
'   M = (n *Sxy - Sx * Sy) / (n * Sx2 - Sx * Sx)
'   b = (Sy - m * Sx) / n
'
'   Where:
'   n = number of points
'   Sx = the SUM of all the X coordinates
'   Sy = the SUM of all the Y coordinates
'   Sxy = the SUM of all (x * y)
'   Sx2 = the SUM of all (x * x)
'
' ---------------------------------------------------------------------
Public Function LeastSquareAnalysis( _
        ByRef m As Double, _
        ByRef b As Double, _
        ByRef data() As Point2d, _
        ByVal nPoints As Long) As Boolean

    LeastSquareAnalysis = False

    m = 0
    b = 0

    Dim sigma_x                             As Double
    Dim sigma_y                             As Double
    Dim sigma_xy                            As Double   ' SUM of all (x * y)
    Dim sigma_x2                            As Double   ' SUM of all (x * x)
    sigma_x = 0
    sigma_y = 0
    sigma_xy = 0
    sigma_x2 = 0

    Dim i                                   As Long
    For i = 1 To nPoints
        sigma_x = sigma_x + data(i).X
        sigma_y = sigma_y + data(i).Y
        sigma_xy = sigma_xy + data(i).X * data(i).Y
        sigma_x2 = sigma_x2 + data(i).X * data(i).X
    Next i

    m = (nPoints * sigma_xy - sigma_x * sigma_y) / (nPoints * sigma_x2 - sigma_x * sigma_x)
    b = (sigma_y - m * sigma_x) / nPoints

    LeastSquareAnalysis = True

End Function

VBA Project

We provide a VBA project that you can download. The project includes the above subroutine and a number of other procedures that …

• Prepare a dummy data set
• Plot the data set as points
• Analyse the data set
• Use the calculated coefficients of a linear equations to draw a line element

To execute the pre-prepared data set, use this key-in:
vba run [RegressionAnalysis]modMain.Main

Another MicroStation VBA enthusiast, Stefan Bernsdorf of Centauron, reacted to comments on the MicroStation Programming Forum. He added code to the VBA project to use a selection set of elements as the data source. You can select a number of elements (ellipses, arcs, cells or zero-length lines), then use this key-in:
vba run [RegressionAnalysis]modMain.LeastSquareLineFromSelectedPoints

Q   How can I fit my survey points to a circle in MicroStation?

A   MicroStation does not provide any regression analysis tools. However, some of the add-on applications may offer tools in that category for specific workflows. This example shows how the result of a solution that creates a best-fit circle. You may have survey points that you want to use to create a best-fit circle …

Circular analysis is quite hard, and the VBA project does not atttempt to solve it. However, the C++ Regression Analysis application can analyse both lines and circles, and furthermore works in both 2D and 3D.

Regression Analysis C++ Application

Note: This code is untested with MicroStation CONNECT

LA Solutions has created a Regression Analysis application (plug-in) for MicroStation CONNECT to perform linear and circular regression analysis in 2D and 3D. This application (Regression.dll) is available for evaluation.

Download VBA Regression Analysis Project

The above code is available in this MicroStation VBA project. Unpack the ZIP archive and copy RegressionAnalysis.mvba to a location where MicroStation can find it. A good place to copy it would be \Workspace\Standards\vba. To create the demonstration plot, key one of the following into MicroStation's keyin dialog …

vba run [RegressionAnalysis]modMain.Main

vba run [RegressionAnalysis]modMain.LeastSquareLineFromSelectedPoints

---

Back to the VBA article index.